The PDF file `chatgpt_walk_net_part1.pdf` documents a project where the author worked with OpenAI’s ChatGPT and Anthropic’s Claude.ai to write Python code for inspecting neural networks. This was part of a larger project applying software reverse engineering to AI.
Here are the key takeaways from the document:
- “Walking” a Neural Net: The core concept is “walking” a neural network, meaning following an input value `x` through each element of the network to produce an output value `y`. This involves tracking how the input is multiplied by weights, added to biases, and affected by threshold functions (like ReLU).
- Interpretable NeuralNet: This work is related to a more complex project called “Interpretable NeuralNet,” which uses “surrogate polynomial coefficients” to understand the formulas learned by a neural network. However, this document focuses on a simpler method of direct inspection.
- Linear Networks: The document starts by examining purely linear networks (no hidden layers). In such cases, the learned formula (y = wx + b) can be directly extracted from the network’s weights (w) and biases (b).
- Hidden Layers and Non-linear Activations (ReLU): When hidden layers and non-linear activation functions like ReLU [rectified linear unit which == max(0,x)] are introduced, the process becomes more complex. The network’s function becomes piecewise linear with “kinks” or breakpoints introduced by the ReLU function. While it’s still mathematically possible to “walk” the network, the resulting formula becomes much more complex, especially with larger networks.
- ChatGPT’s Role: The document includes excerpts of conversations with ChatGPT, showcasing how the AI chatbot helped in writing the Python code, explaining concepts, and troubleshooting issues.
- Illustrative Examples: The document provides Python code examples that demonstrate these concepts, including creating synthetic data, training small neural networks, and “walking” their weights. There are also discussions about how random initialization, gradient descent, and other aspects of neural network training work in practice, and how they relate to the actual code being written and executed.
- Square Root Example: A significant portion of the document focuses on creating a small neural network that learns to approximate the square root function (y = sqrt(x)). This example further illustrates the complexities introduced by ReLU activations.
- Limitations: The document emphasizes that while the “walking” approach is possible for small networks, it becomes practically intractable for larger, more complex architectures due to the combinatorial explosion of possible piecewise regions.
In essence, the document details an exploration of how to understand what a neural network is doing internally, by directly examining its weights, biases and the effects of threshold functions, how this can be done in simple case, how this process is made dramatically more complex by non-linear activation functions in deeper networks, and illustrating how AI can assist the process of exploring this kind of reverse-engineering.
I’ve been getting heavily into AI-generated summaries, which often trigger a “hmm, this summary is very good, but it’s missing these three points which are more important” — and I likely wouldn’t have thought of those three points without first having seen the AI summary. So, here is how I summarized Part 1, after reading several AI-generated summaries, including the one above:
- Large language models (LLMs) such as ChatGPT, Claude, and Google Gemini, are, at bottom, neural networks.
- Even the largest neural net, like ChatGPT itself, after its has been trained with sample data, computes a function: y=f(x) .
- A neural net can approximate the effect of a function such as square root (and log, tan, etc.), without ever knowing that’s the function it is approximating, and based only on some sample (x,y) training data that was generated by the function.
- Neural networks are overly opaque (non-transparent) for many applications: while the net can amazingly compute all manner of things (including an appropriate next word in a sentence), they are currently much less good at telling us how/why they arrive at their y outputs, given x inputs.
- However, they are not totally opaque; neural networks can be reverse engineered.
- In addition to applying post-hoc analysis to neural networks, such as surrogate polynomial coefficients, in certain limited cases one can “walk” through the neural net to extract the formula a neural net has learned, directly from the net’s weights/biases.
- Any non-trivial neural net, once it uses nonlinear activation functions such as ReLU, will contain “kinks” or regions; each seem between regions is marked by an activation function.
- We don’t want a neural net to memorize its (x,y) training data; we want to net to learn the (x,y) relationship, which is very different; we don’t want the effect of a lookup table; instead, we want something that can predict y give input values x the net hasn’t seen before; we want neither “overfitting” nor “overfitting”; we want the net to learn both accuracy and generalization.
- We saw an extended example of interacting with an AI chatbot like ChatGPT to produce code and assess its output, when the user runs the code locally.
Topics discussed here in Part 2 include:
- Apply net-walking from small neural nets representing numeric data to those representing text
- Similarities and differences from LLMs
- Walking a tiny toy language model
- What text “embeddings” represent in the tiny language model, compared/contrasted with embeddings in LLMs
- Temperature, argmax/softmax, logits, sampling, and selecting the next token from a list of the most-probable next tokens
- Historical comparison of finding square root by guessing/iterating, with the neural net’s method of training/error-adjusting weights
- The centrality of error-correction (nets may be doing pattern recognition, but the way they get there is via error correction)
- The 768 “sweet spot”
- The separate roles of backpropagation vs. the optimizer
- Transformers and “attention” are NOT performing recurrence, though it can appear that way in a chat
- Transformers like ChatGPT are in some ways “just like” our tiny neural networks (except for the ways in which they’re not)
- Tweaking a neural net’s parameters to avoid local minima
Applying net-walking from small numeric neural nets to (equally small) text nets, with applicability to LLMs
Below, my prompts and commentary in italics. In addition to ChatGPT’s responses, I’ve sometimes also included material from the right-hand “chain of thought” (CoT) panel that appears if you click on e.g. “Thinking for 7 seconds”. [Whether such explicit CoT statements in prose truly reflect an underlying sequence of reasoning steps, and if so, whether prose is the best way for CoT to be implemented, is discussed in “Worries about latent reasoning at LLMs” at the LessWrong blog re: Meta’s COCONUT (Chain of Continuous Thought); see also my CoT page.]
In an earlier session, ChatGPT had built a nice small Python script for me as described in a summary I asked it to generate in an attempt to carry over “state” or “memory” from one session to another:
“Multi-layer / Nonlinear: We demonstrated a small ReLU net with a handful of neurons and manually ‘walked’ the weights to show how an input flows through each layer, forming a piecewise (ReLU) expression.”
AS (long multi-paragraph prompt):
That earlier small net did a good job modeling y=sqrt(x), basically achieving the effect of regression on the (x,y) training numbers, but not using top-down regression formulas, and instead simply learning square root.
I now want to discuss the extent to which what is learned from a small numeric net like that can be applied to a LLM, such as yourself ChatGPT. Is it safe to say that you ChatGPT (or other LLMs like Claude) are doing essentially the same thing that our tiny toy neural network did, although on a monumentally larger scale? Might I describe you as performing a y=f(x) function, where x is e.g. text like what I’m typing right now, converted to numbers in some way (word or sentence embeddings??), input to your model, and coming out as predicted next word/phrase/sentence, then fed back in for more (using attention/transformer which I’d prefer to not get into at the moment if possible)?
This is probably very superficial. I haven’t mentioned how your y=f(x) gets trained in the first place (though I assume backpropagation, error correction), and I haven’t mentioned subsequence training that might occur in tool use, data analysis, even reasoning (to the extent that doesn’t simply come “for free” with your basic training).
But please walk me through what one could learn from small toy numeric neural nets might still be applicable to an LLM giant working with text or images, as well as numeric user input.
ChatGPT:
[Thought about small nets and LLMs for 31 seconds:
Drawign [sic] connections
I’m examining the similarity between “toy numeric networks” with ReLU regression and large language models like ChatGPT, focusing on how both predict outputs based on inputs.
Connecting concepts
Interestingly enough, small toy networks and large language models share core function approximation principles, despite their distinct inputs, architecture, and scale.
Understanding structures
I’m noting that neural networks, whether feed-forward with ReLUs or Transformer-based, both function as function approximators and are trained using gradient-based methods.
Mapping connections
I’m working through the iterative training of neural networks, their increasing complexity with layers, and constant progress towards sophisticated pattern recognition. Adjusting parameters and activation functions are crucial steps.
]
At a high level, all neural networks — be they tiny MLPs learning sqrt(x) or massive language models like ChatGPT — are doing the same fundamental thing: function approximation. In other words, given an input x, the network produces an output y = f(x). The differences arise mostly in:
- What the inputs and outputs represent
- How large/complex the network is
- How it’s trained and what data it’s trained on
- What architectural features help it handle very large or complex input domains (e.g. text sequences, images, etc.).
Below is a “walk-through” explaining what carries over from a small numeric net to a giant LLM, and what changes.
1. The Essence: A Learned Mapping
In your toy ReLU network for sqrt(x):
- Input: a single scalar x
- Hidden layers: a handful of neurons, each computing a linear transform plus ReLU
- Output: a single scalar ^y that the net tries to match to sqrt(x)
Under the hood, you have parameters (weights, biases) that get adjusted via gradient descent and backpropagation to minimize some loss like (^y – sqrt(x))^2. [^y = hat y, or predicted y]
How LLMs Are Similar
- They also have inputs and outputs: The input is a sequence of tokens (words or subword pieces) converted to numeric embeddings; the output is a distribution over the next token(s).
- They also have layers of parameters: Instead of a few layers and a handful of neurons, LLMs have many layers and thousands (or billions) of hidden dimensions.
- They also learn via gradient-based optimization: They start with random weights, see vast amounts of text, and iteratively adjust parameters to minimize a next-word prediction loss.
Hence the fundamental concept is the same: find the parameter set W that best approximates a mapping f(x). Whether x is “the current text so far” or a single numeric value, the approach is mathematically quite similar. [This similarity also applies to the target/output value, whether y is sqrt(x) or the next word/token/phrase.]
2. Input Encoding
For the toy network: You fed in a plain number x.
For an LLM: The “plain text” (characters or tokens) is first turned into embeddings — vectors of real numbers. This is analogous to feeding sqrt(x)-net a single real number, but on a far grander scale: each token is represented by, say, a 768-dimensional embedding (or 1024, or more). [See embeddings discussed later in this web page; in our tiny text net here, we have only 2 dimensions (hidden_dim=2 in tiny_text_net.py .]
In both cases, you end up with vectors of real numbers as the raw “food” for the network. The difference is just dimensionality and how we construct those embeddings.
3. Output Interpretation
For your sqrt(x)-net: The output was also a single real number, and you interpret it as the approximate sqrt(x).
For an LLM:
- The network outputs a large vector of logits (one entry per possible token).
- We convert those logits to probabilities (via softmax) for each possible next token. [See logits and softmax discussed later in this web page.]
- The model “chooses” (or samples) the next token based on these probabilities.
In essence, it’s still a numeric output. It’s just that we interpret the numeric output as a probability distribution over a giant vocabulary. [See tiny_text_net.py]
4. Piecewise / Nonlinear Structure
A small ReLU net can be piecewise linear when we manually expand it. An LLM is typically built from many layers of multi-head attention, feedforward blocks (often with ReLU or GeLU activations), residual connections, etc. But the same principle holds:
- Each activation function (like ReLU or GeLU) introduces nonlinearity.
- Each linear or attention head is still a linear transform with a huge weight matrix.
Put enough of these together, and you can approximate extremely complicated functions.
[AS (later follow-up): You earlier said, “Each activation function (like ReLU or GeLU) introduces nonlinearity.” Give me a sentence or two on why that is desirable. Is it simply in order to be able to map non-linear x/y relations, such that it doesn’t serve a purpose for mapping linear relationships? Or does everything, even the simplest seemingly linear x/y relation, turn out in a neural net to benefit from non-linearity, or what?
ChatGPT:
Short Answer:
Neural networks must include nonlinear activations (ReLU, sigmoid, etc.) to capture nonlinear relationships in data. Without these nonlinearities, a network of stacked linear layers collapses to a single linear mapping, severely limiting the functions it can learn.
1. Why Nonlinearity Is Essential
Expressiveness:
— A stack of purely linear layers (like Linear -> Linear -> Linear) effectively collapses to one linear transformation.
— By adding a nonlinear activation (e.g., ReLU) between layers, the network can bend the input–output mapping into curves, corners, or more complex shapes.
Universal Approximation:
— The theoretical power of neural nets as “universal approximators” relies on having nonlinear elements.
— Without nonlinearity, the net can’t approximate complicated functions like y=sqrt(x), classification boundaries, or anything else that isn’t straight-line mapping.
Practical Impact:
— In many real problems (like image classification, language modeling, etc.), input–output relationships are far from linear. Nonlinear activations allow the net to learn those complexities.
— Even for simpler, mostly linear tasks, mild nonlinearity often helps the network converge faster or capture slight deviations from perfect linearity.
2. Do Simple Tasks Benefit from Nonlinearity?
— If your data truly is perfectly linear (say y=2x+3), technically a linear-only network (one layer, no activation) can learn that exactly.
— But in practice, real-world data rarely aligns to a perfect linear form. Even “simple” relationships might have nuances.
— Therefore, most neural nets keep a nonlinear activation by default, because it makes the model more versatile. If the data really is linear, the network can still approximate it. If it isn’t, the network can adapt to those extra complexities.
]
5. Iterative Training and Error Correction
Both systems use backpropagation and an optimizer (like SGD, Adam, etc.) to repeatedly: [See explanation below of the difference between backpropagation and the optimizer.]
- Make a forward pass: compute ^y=f(x).
- Compare ^y to the target (for LLMs, the target is “the next token in the sequence”). [During training, the next token, or a masked token, are known.]
- Compute a loss.
- Do a backward pass: compute gradients (∂loss / ∂W) .
- Update the weights to reduce the loss.
Whether you’re learning sqrt(x) or next-word prediction, it’s the same cycle — just repeated millions or billions of times on massive text corpora in the LLM case.
6. Why the “Toy Net” View Is Still Instructive
- Universal Approximation
A tiny ReLU net (with enough hidden units) can approximate just about any continuous function in 1D, 2D, etc. [See here for brief discussion of the Universal Approximation Theorem (AUT); note “continuous” limitation.]
LLMs extend that idea to function spaces mapping from sequences of tokens to next tokens. The “same rules” (linear transformations + activation + large data + iterative optimization) let the net approximate language patterns. - Layers as Feature Builders
In a tiny net, each hidden layer might successively capture more refined “features” of x. In LLMs, each layer can be viewed as building richer contextual features of the entire input text. The concept—transformation of raw input into increasingly abstract features—remains the same. [See (forthcoming) for discussion of “features” captured by, or least said afterwards said to be captured by, neural nets.] - Overfitting vs. Generalization
Even in your small net, you might worry about overfitting if you have too many neurons or train too long on too few data points. LLMs can overfit too (though typically they’re trained on so much data that they instead face issues of memorizing rare training examples). - Interpretability Challenges
Even with a small net, expanding out all the piecewise expressions can get unwieldy. With an LLM, interpretability is even harder. The difference is mostly scale and architectural complexity, but the fundamental “black box” nature is similar.
7. The “Next Word” Aspect
One thing that distinguishes language models is the sequence aspect: they have to repeatedly apply the function for one token at a time, or sometimes for many tokens in parallel, to get the next token. It’s akin to feeding the output back in as part of the next input. But at each step, there’s still a big forward pass: “Given all tokens so far, produce the next token distribution.” This yields a chain of predictions that forms the conversation. [Somewhat akin to feeding the output back in, but NOT recurrent: see discussion below of transformers/attention.]
8. Omitted Topics (But Still Important)
You mentioned you’d rather not dive deeply into attention or the internal workings of the Transformer. That’s perfectly fine: just know that the basic building blocks—linear transformations, “activation” functions, many layers, big weight matrices—are conceptually the same as your toy net. The attention mechanism is a specialized layer that helps the model handle long-range dependencies in text more efficiently than a simple MLP. But it still stands on the same neural network foundation. [See below for more detailed discussion. Note here how ChatGPT makes sure I don’t completely sweep this under the rug.]
9. Summary
- Core Concept: Both your small numeric net and a large language model are neural nets that learn parameters to approximate a function from input (numbers or text embeddings) to output (predicted number or next-token distribution).
- Scale: LLMs have orders of magnitude more parameters, training data, and architectural complexity (many layers, attention blocks, massive parallelization).
- Training Loop: Fundamentally the same: forward pass, compute loss, backward pass, update weights.
- Applicability: Studying small nets clarifies how neural networks “build” a function internally, how weights are updated, and how nonlinearity + linear combos approximate functions. Those ideas absolutely carry over to LLMs, just scaled up dramatically.
Ultimately, everything you learn about how your toy net approximates sqrt(x) does apply to how giant models approximate “the next word.” The differences are mostly in the details of architecture, training scale, and the complexity of the input/output domains.
Walking a tiny toy language model
AS: Is there some way a tiny test could be written, as similar as possible to the toy ReLU network for sqrt(x), but that handled text input/output in some way? The toy ReLU network “walked” the weights/biases of the net to show how the net after training is used to predict sqrt(x). Let me show you what output looks like: [Showed this ChatGPT session the same “python walk_sqrt_net_2.py” output as shown above.]
Is it foolish to think something like this could be done with a little bit of text?
ChatGPT:
[Thought about toy model for text for 5 seconds
Envisioning a neural network
I’m thinking through a small text-based neural network, using minimal embeddings and ReLU layers to map input tokens to output tokens, while avoiding overfitting.
Visualizing transformations
I’m mapping out a tiny text-based neural network with small embeddings and ReLU layers, demonstrating how it transforms input tokens through a brief code snippet and a mini dataset.
Coding up the solution
OK, let me see. I’m coding a small neural network in PyTorch, outlining each layer’s expansion. The example, though limited, effectively demonstrates the process.]
Not at all foolish! You can create a toy neural net for text that is analogous to your 2×2 ReLU net for sqrt(x). Of course, text is more complex than a single number, but the principle remains:
- Convert text to a numeric representation (e.g., a small embedding).
- Pass that through a couple of ReLU (or other) layers.
- Produce an output distribution over tokens (or a single “predicted token”).
- “Walk” the trained net by expanding the linear transformations + ReLUs exactly like you did with sqrt(x).
Below is a contrived end-to-end example in PyTorch to demonstrate the idea. We’ll keep the vocabulary extremely small (like 3–5 tokens) and train on a silly “dataset” just to illustrate. After training, we’ll do a forward pass manually in python, printing each intermediate activation. This is only to show that it’s possible—it’s definitely not a useful text model!
1) Setup and Dummy “Dataset”
We’ll imagine we have a vocabulary of just 5 tokens:
["hello"]["world"]["cat"]["dog"]["!"]
We want a toy network that tries to map "hello" to "world" and maybe "cat" to "dog", so we have some minimal variety. We’ll train it as if it’s a next-token prediction. That is:
- Input: a single token index
- Output: distribution over next token index
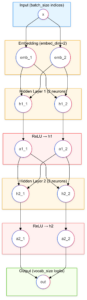
2) Define a Very Small Network
We’ll make this as close in spirit as your 2×2 ReLU net as we can, but we need:
- An embedding layer (to turn token indices into a small vector).
- A couple of linear/ReLU layers.
- A final linear layer that outputs logits over the entire vocabulary.
Architecture:
- Embedding dimension = 2 (just to keep it tiny).
- Hidden layer 1 = 2 neurons (ReLU).
- Hidden layer 2 = 2 neurons (ReLU).
- Output layer = 5 logits (for 5 tokens).
3) Train the Tiny Net
We’ll do straightforward classification: each input token tries to predict the correct next token. We’ll run for a few hundred epochs and see if it memorizes these handful of pairs.
4) Check Predictions
We can see if the model produces the correct next tokens:
[Code in tiny_text_net.py; see link below]
Ideally, we’ll see something like:
hello -> world
cat -> dog
dog -> !
world -> !
…assuming it memorized those pairs.
5) “Walk” the Network, Layer by Layer
Just like your sqrt(x) net, we can do a manual forward pass for a single token and print the intermediate expressions. (We won’t do a piecewise “closed-form” expansion, because it includes an embedding lookup—i.e., a table of weights. But we can demonstrate exactly how each step transforms the data.)
[manual_forward() function, collected with all preceding code in tiny_text_net.py]; see also tiny_text_net.ipynb in Google Colab.]
Explanation of each step:
Embedding: The model looks up a 2D vector for “hello.” Let’s say that ends up being something like [+1.2,-0.7]. That’s your “x” for the next layer. [See later discussion of embedding.]
Layer 1:
z1 = W1 @ emb_vec + b1. This yields a 2D vector. [In Python 3.5+, “@” is the matrix multiplication operator.]
Then a1 = ReLU(z1).
Layer 2:
z2 = W2 @ a1 + b2, again 2D.
a2 = ReLU(z2).
Output layer:
z_out = Wout @ a2 + bout, which is 5D (one logit per vocab token).
The largest logit is the predicted next token.
You’ll see numeric values for each step, just like you had for sqrt(x). This is the same conceptual “walk-through.”
Caveats / Observations
Closed-form expansions
With your sqrt(x) net, you wrote the piecewise expansions. Here, we could do it, but we’d have to expand the embedding lookup as:
emb_vec =E [x_idx] = (E [x_idx,0], E [x_idx,1] )
plus the linear transformations. Nothing stops us from writing it out, but it becomes less intuitive to read.
Just a Memorization
This toy is basically memorizing “hello → world”, “cat → dog,” etc. It’s not “learning language.” But it demonstrates you can treat token input as numeric, pass it through a small net, and do a manual forward pass.
Scaling
Real language models do the exact same steps but with:
- Larger embedding dimensions (hundreds or thousands) [And embeddings used in genuine language models try to features (such as the word’s location in a given sentence, and the word’s commonness/rareness (inverse frequency) in the entire vocabulary); in our tiny example here, it merely represents an arbitrary location in a 2D space. See the “Embeddings in the tiny text net” section below, and material on patent claim embeddings.]
- Many more layers (dozens or hundreds)
- Attention blocks in place of (or in addition to) simple linear layers
- Millions/billions of training examples
Despite these differences in size/complexity, you can still break down a bigger model step by step—though for something like GPT-sized nets, that’s obviously unwieldy by hand.
In Conclusion
It’s absolutely possible to replicate the “manual step-by-step ReLU analysis” style on a tiny text-based network. The main difference is that you first have to embed tokens into numeric vectors, then do the same forward pass expansions. Even though it’s contrived, it helps cement that a language model is, at bottom, still a big function tokens → next-token distribution built from linear transforms + nonlinearities (and in real LLMs, attention blocks).
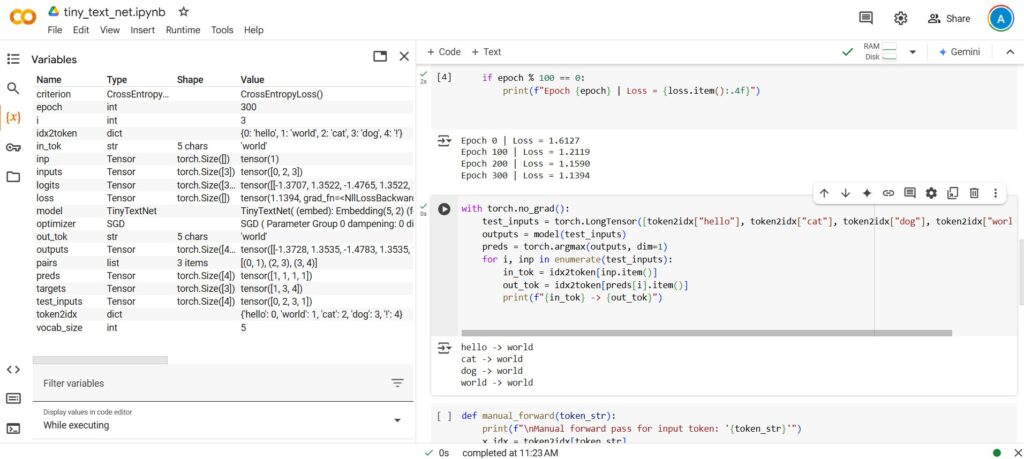
AS: Seems to have worked, right out of the box. I put the 4 pieces together, and:
C:\work\ml>python tiny_text_net.py
tensor([0, 2, 3, 1]) tensor([1, 3, 4, 4])
Epoch 0 | Loss = 1.3034
Epoch 100 | Loss = 0.5625
Epoch 200 | Loss = 0.1169
Epoch 300 | Loss = 0.0389
hello -> world
cat -> dog
dog -> !
world -> !
Manual forward pass for input token: ‘hello’
Embedding vector for ‘hello’: [ 1.2167829 -1.0983902]
LAYER 1 (z1): [-0.81962353 -1.3901908 ]
LAYER 1 (a1 = ReLU(z1)): [0. 0.]
LAYER 2 (z2): [-0.00322088 2.0367088 ]
LAYER 2 (a2 = ReLU(z2)): [0. 2.0367088]
OUTPUT LAYER (logits): [-0.9125997 5.260045 -1.6363995 -3.1030662 2.535739 ]
Predicted token: world
Can you walk me through what’s happening here? I think you start with the embedding for “hello”, that embedding gets transformed in Layer 1, then in Layer 2, and then in the output layer we have a choice of 5 (?) different most-probable ones to pick, we pick the max probable, and then look up the embedding in idx2token[] and print it?
ChatGPT:
Here’s a step-by-step “tour” of what your tiny text model is doing under the hood when you pass in the token "hello" and end up with the predicted token "world".
1. Embedding Lookup
Input Token: "hello"
Token Index: 0 (since "hello" was mapped to 0 in your token2idx dictionary)
- The embedding layer is basically a lookup table of shape [vocab_size,embed_dim]. [Contrast genuine embeddings in LLMs; see below.]
- Since the index for
"hello"is 0, we grab the 0-th row of that table.
In your printout:
Embedding vector for 'hello': [ 1.2167829 -1.0983902]
So internally, the model represents "hello" by the 2D vector [1.2167829,−1.0983902].
2. First Linear + ReLU (Layer 1)
Next, we take the embedding and pass it through the first linear layer:
z1 = W1 ⋅ emb_vec+b1 (where W1 is a [2×2] weight matrix, and b1 is a 2D bias vector). [Note that ⋅ is dot product.]
Your code shows:
LAYER 1 (z1): [-0.81962353 -1.3901908 ]
LAYER 1 (a1 = ReLU(z1)): [0. 0.]
- z1 is simply the result of the matrix multiply + bias.
- a1 is the output of passing
z1through a ReLU, which zeroes out any negative values.
Here, both entries of z1 are negative (−0.82 and −1.39), so the ReLU sets them to 0. Hence,
a1=[0,0].\mathbf{a}_1 = [0, 0].a1=[0,0].
3. Second Linear + ReLU (Layer 2)
We then feed a1 into the second linear layer:
z2 = W2 ⋅ a1 + b2
Since a1=[0,0], the matrix multiplication part W2 ⋅ a1 will be all zeros, so z2 comes solely from the bias b2.
Your printout:
LAYER 2 (z2): [-0.00322088 2.0367088 ]
LAYER 2 (a2 = ReLU(z2)): [0. 2.0367088]
- The first entry is negative (−0.0032), so ReLU sets it to 0.
- The second entry 2.0367 is positive, so it survives.
Therefore, a2=[0,2.0367088].
4. Output Layer (Logits)
Finally, we take a2 and pass it to the output layer:
zout = Wout ⋅ a2 + bout
- Wout has shape [5×2] because we have 5 possible tokens in the output.
- bout is shape [5][5][5].
Result:
OUTPUT LAYER (logits): [-0.9125997 5.260045 -1.6363995 -3.1030662 2.535739 ]
So we have 5 numbers (logits), one per possible token: [hello, world, cat, dog, !]. These logits are not probabilities yet, but a higher logit means a higher probability after softmax.
[Logits and softmax, and their relationship to balancing the variety and accuracy of a net, are discussed below.]
5. Picking the Most Probable Token
[See below on choosing among multiple probable tokens]
Your code (via torch.argmax) picks the index of the largest logit:
Predicted token: world
The largest logit is 5.260045 at index 1, which corresponds to "world".
Hence, from the input "hello", the model’s final answer is "world".
Recap
- Lookup: Turn token
"hello"into the 2D embedding[1.2167829, -1.0983902]. - Layer 1: Multiply by
W1, addb1→ negative results → ReLU sets to[0,0]. - Layer 2: Multiply by
W2, addb2→[-0.0032, 2.0367]→ ReLU →[0, 2.0367]. - Output: Multiply
[0, 2.0367]byW_out, addb_out→ 5 logits. The largest logit indexes"world".
So conceptually, it’s exactly the same forward-pass procedure as with your sqrt(x) net — just with an embedding lookup instead of a direct numeric input, plus an output dimension of 5 tokens instead of 1 real number. Everything is still matrix multiply → bias add → activation at each layer.
An example of AI chatbot working through a user’s misunderstandings
[Below, note explicitly prompting ChatGPT to not just agree with me even if I’m close enough. LLM tendency to over-agree with users has been observed as part of the well-known LLM “hallucination” problem; this tendency could relate to incorporation of the user’s text as part of the next prompt; see “Transformers & attention do not employ recurrence” below.]
AS: It sounds like my attempted explanation was pretty far off. Can you point specifically to what I misunderstood in:
>>> I think you start with the embedding for “hello”, that embedding gets transformed in Layer 1, then in Layer 2, and then in the output layer we have a choice of 5 (?) different most-probable ones to pick, we pick the max probable, and then look up the embedding in idx2token[] and print it
?
Your summary is actually pretty close to what’s happening! The only real subtlety is how we get from the final network output (the logits) to a token string. Specifically:
- You do start with the embedding for
"hello". - That embedding does get transformed by Layer 1 and Layer 2 (via matrix multiplication + bias + ReLU).
- The final output layer does produce 5 logits, one for each possible token in the vocabulary.
- You do pick the token with the highest logit (via
argmax). - You do then map that token index (not embedding) to a token string via
idx2token[...]to print it.
So the flow you described is fundamentally correct.
What Might Have Been Confusing
1. “Looking up the embedding” vs. “Looking up the token string”
When you say, “we pick the max probable, and then look up the embedding in idx2token[],” that sounds slightly off—idx2token is just a dictionary that turns the predicted token’s integer index into the token string (e.g., 1 -> "world"). It doesn’t look up another embedding; it’s just looking up the string label.
Hence:
- Embedding is used at the network input step.
idx2tokenis used at the output step, purely to convert the integer index (0, 1, 2, 3, 4) into a human-readable token ("hello","world", etc.).
2. ReLU Zeroing Out in Layer 1
In your specific result, the net’s first layer spit out negative values, so the ReLU turned them into [0, 0]. That means that effectively Layer 1 did nothing for "hello"—the second layer is just operating on [0, 0] plus its bias. Then that second-layer output goes into the final layer. You might not have realized that everything hinged on the bias in Layer 2. [AS: I like the colloquial “spit out,” and the helpful “You might not have realized that everything hinged on…”]
3. Vocabulary Size, Logits, and Probabilities
You mentioned “we have a choice of 5(?) different most-probable ones.” Indeed, that’s correct—there are 5 tokens in the vocabulary, so the model’s output layer always produces 5 logits. Whichever logit is largest becomes the predicted token index.
But strictly speaking, we usually convert logits to probabilities with softmax if we want to treat them as a probability distribution. In code (when just picking the top token), we often skip the explicit softmax step and just do argmax(logits) because the largest logit also yields the largest probability under softmax.
Bottom Line
Your explanation:
“I think you start with the embedding for ‘hello’, that embedding gets transformed in Layer 1, then in Layer 2, and then in the output layer we have a choice of 5 different most-probable ones to pick, we pick the max probable, and then look up the embedding in
idx2token[]and print it?”
…is essentially correct. The only minor wording tweak is that in the last step, we look up the token string (not an embedding) in idx2token[], using the integer from argmax. That’s why the final output is "world". Other than that small distinction, your mental model of the process is spot-on.
ChatGPT: Let’s untangle a couple of points here. You’re absolutely right that the array of logits is: [AS: ChatGPT being a good teacher: here’s where you’re right, but let’s untangle this…]
[-0.9125997, 5.260045, -1.6363995, -3.1030662, 2.535739 ]
Indexing them in 0-based Python style:
- index 0 → −0.9126-0.9126−0.9126
- index 1 → +5.2600+5.2600+5.2600 ← largest value
- index 2 → −1.6364-1.6364−1.6364
- index 3 → −3.1031-3.1031−3.1031
- index 4 → +2.5357+2.5357+2.5357
So when you do:
pred_token_idx = torch.argmax(z_out).item()
argmaxreturns the index of the largest logit.- Here, the largest logit is 5.26005.26005.2600 at index 1.
That’s why pred_token_idx should be 1, and therefore idx2token[1] is "world".
Why Doesn’t It Return 0?
- If the largest value had been at index 0 (say the logit array was something else), then the answer would be index 0, which maps to
"hello". - But in your actual array, index 1 is the largest.
So if you see something saying “argmax → 0,” that would be a mismatch with the logit array you pasted. Possibly you were just reading the array from left to right and thought “the first element is biggest.” But in fact: [Again, see how ChatGPT tries to think its way into possible reasons for my confusion.]
- -0.9126 is less than 5.2600
- 5.2600 is definitely the largest
- Indices 2 and 3 are even more negative
- Index 4 (2.5357) is positive but still less than 5.2600
Hence, the largest is at index 1, yielding "world".
What Are Logits, Anyway?
[Above is ChatGPT’s own colloquial subhead. I said “maybe I don’t understand what logits are”, and it in part responds with this subsection of text. More on logits below.]
A logit is just the raw (unnormalized) score a neural network spits out before any softmax.
- You can turn logits (ℓ0,ℓ1,…,ℓn−1) into probabilities via: pi=eℓi∑j=0n−1eℓ [[TODO: fix formula]]
- The token with the highest logit also has the highest probability after the softmax.
- That’s why
argmax(logits)is sufficient to pick the most likely token (no need to explicitly compute the softmax if you only want the single best choice). [See discussion below on temperature, argmax/softmax.]
So in short:
- Logits are the final numeric “scores” for each possible token.
- Argmax picks whichever score is largest.
- We then convert that integer index into a readable token string using
idx2token[index].
And that’s exactly how you go from
OUTPUT LAYER (logits): [-0.9125997 5.260045 -1.6363995 -3.1030662 2.535739 ]
to
Predicted token: world
because index 1 corresponds to "world".
No worries at all! That “Aha!” moment is exactly how it goes for many of us when we first see raw logits and manually parse which index is largest. The key points are:
- Logit array: A score per possible token.
- Argmax: Finds the index of the highest score.
- Vocab mapping: That index is looked up in
idx2token[]to get a text label (e.g.,"world").
Everything else (e.g., negative numbers, the presence of a big positive for index 1, etc.) is just standard neural-network output. The biggest logit wins!
[Thought about temperature in logits for 4 seconds]
Yes, exactly—temperature is a parameter that modifies how we turn logits into a probability distribution. It can make the model’s sampling more or less “greedy.”
How Temperature Works
Normally, to convert logits ℓi into probabilities for token i, we apply the softmax:
p i = e ^ ℓi / ∑j ^ e ^ ℓj
But if we introduce a temperature parameter T>0, we rescale the logits by 1 / T:
p i = (e ℓi / T) / ∑j ^ e ^ (ℓj /T)
- If T=1, we get the usual softmax (no change).
- If T<1, we’re dividing by a number less than 1, so the exponent ℓi/T gets larger in magnitude for any nonzero ℓi. The distribution becomes sharper, and the model is more likely to pick the single best token (greedy).
- If T>1, the logits get “flattened,” and the differences between them matter less. The model’s distribution becomes smoother, and it’s more likely to sample lower-probability tokens.
Impact on Which Token Is Chosen
- If you always do
argmaxof the logits (greedy decoding), you ignore temperature and never sample. - If you sample from the softmax distribution, then temperature affects how “certain” or “exploratory” the model is. At higher temperatures, you get more variety; at lower temperatures, you get more repetition of the most likely token.
Hence, yes, with a temperature-based sampling scheme, you don’t always pick the highest logit — sometimes you pick a token with a lower logit but nonzero probability, especially if the temperature is high.
A little history, and the centrality of predictive error correction
AS: The expansion [in Part 1] of calculating sqrt(8) or whatever looks like something that people might have done by hand many centuries ago? Well, maybe not: the idea of guessing at a square root, multiplying it by itself, comparing to x, and then increasing or decreasing the guess probably emerged pretty naturally. But do you know of any really ancient method that looks even vaguely like what we’ve got here?
ChatGPT:
Thought for 12 seconds [“I explored ancient methods like the Babylonian method and the abacus method, alongside book suggestions on neural networks. It’s interesting to see the progression from early techniques to modern approaches.”]
Historical or “Ancient” Methods for Computing sqrt(x) That Resemble a Neural Net
The Ancient/Babylonian (Newton) Method
Babylonian Method (a special case of Newton’s method) is probably the oldest well-documented algorithmic approach to approximating square roots. You start with a guess, g, and iteratively update:
g_new = 1/2 (g_old + (x / g_old))
This is effectively a feedback loop that keeps refining the guess.
Comparing to a Neural Net
A ReLU net (or any neural net) is doing a series of weighted sums and nonlinear transformations. Once trained, it computes sqrt(x) by feeding x forward through those layers.
In contrast, Newton-like methods compute sqrt(x) by iteratively refining one or two scalar guesses, using derivatives or expansions. It’s not structured as a multi-layer “spreadsheet” of partial sums and ReLUs.
So historically, you won’t find a direct “layer by layer, piecewise linear transformation” approach to computing square roots in, say, ancient Babylonian or Greek mathematics. Their iterative approach is more like “guess -> refine -> refine”.
Neural networks, on the other hand, compile a (potentially complicated) function into weights. That’s a concept that didn’t exist historically—at least not in extant documents.
Short Answer: No ancient or centuries-old method is known that explicitly does something akin to “hidden layers with linear transformations + thresholding” for square roots. Iterative guess-and-check (Newton’s method) has been around for millennia, but it’s a different conceptual framework.
AS: Interesting that as far back as the Babylonians, people knew the smart Newtonian way to do this. Hmm, backprop is a bit like this, no?: make a guess/prediction, see how compares to know correct answer, adjust up or down depending on whether you were too high or too low, try again, with a guarantee of sorts you’ll get closer. Iterative error correction: one could do a lot worse….
[I was thinking here of a fragmentary quotation from the cybernetics pioneer W. Ross Ashby, as quoted in Mind Design III : “The whole function of the brain is summed up in: error-correction.” (see Ashby aphorisms #41.) See also Hohwy, The Predictive Mind (2013), ch.2: Prediction error minimization; ch.3: Prediction error, context and precision.] [[TODO: something on how this can be directly made operational; cite Andy Clark books from the 1990s on connectionism & error correction.]]
ChatGPT: … Indeed, backprop and Newton’s method share that broad idea of iteratively refining something based on how “off” you are. Of course, in neural nets, the “guess” is a large set of weights and biases, but the principle — observe error, compute gradient, adjust — parallels the ancient iterative methods in spirit…. we often think neural nets are magical, but mathematically they’re not so different from iterative improvement methods that have existed for centuries — just scaled up for many parameters and with multiple layers….
Embeddings in the tiny text net
"hello") gets assigned its own “row” in a learnable weight matrix. That row—an array of real numbers—serves as the **numeric representation** of that token inside the network.- **Think of it as a coordinate**: The vector
[1.2167829, -1.0983902]is just a 2D point in some abstract space where “semantic relationships” can (in principle) be captured. - **Learned through training**: The network adjusts all these embedding vectors during training so that tokens used in similar contexts (in real applications) end up with embeddings that help the model do its prediction task. (In this toy example, it mostly just memorizes which token should come next.)
- **Purpose**: These numbers are then fed into subsequent layers (linear + ReLU, in your case), letting the model transform from “token ID” to “features relevant for predicting the next token.” So the short answer: **that 2D vector is how the neural net internally encodes the token “hello”** so it can do math on it (matrix multiplications, ReLU, etc.) instead
Your request was flagged as potentially violating our usage policy. Please try again with a different prompt. [AS: don’t know what was inappropriate about my request, but anyway, got enough of an answer, including the parts I’ve bolded.]
In this toy example, those two embedding dimensions don’t really represent anything “linguistic” or “semantic” in the usual sense—there’s no deeper significance like “first dimension is part-of-speech” and “second dimension is frequency.” They are simply learnable parameters the network uses to help it predict the next token.
Because we have so few tokens (and such a small training set), the embedding layer is mostly just “storing” the information needed to map each input token to its target. With more data (and more tokens), embeddings can start to capture interesting statistical/semantic relationships. But in a toy scenario:
- They’re Arbitrary Coordinates
The two numbers are just a point the network discovered is useful for reducing the training loss on your 4 input–target pairs. With so little data, there’s no strong incentive to learn embeddings that correspond to intuitive axes (like frequency or sentence position). - No Intrinsic Meaning per Dimension
In a real NLP model (with a large corpus), you might see emergent properties in high-dimensional embeddings (e.g., synonyms clustering together). But here, each dimension is simply part of a small parametric “slot” that the net can tweak via gradient descent. The network ends up using them in whatever way helps it produce the correct next token. [AS: “synonyms clustering together,” i.e. with embedding vectors with smaller distances from each other, would be a genuine “feature” learned by, and incorporated in a neural not, in contrast to a post hoc explanation (see brief comment below).] - Analogy: A “Key-Value” System
You can almost think of it like a hash table with continuous keys: each token is assigned a learned vector key, which the later layers use to produce the correct output. Because it’s only 2D, it can’t capture much nuance—just enough to differentiate “hello” from “cat,” etc.
So if you see a 2D embedding like [1.2167829, -1.0983902], you can’t typically say “the first coordinate is word frequency, the second is some morphological property.” Instead, it’s just a pair of real numbers that happen to work to minimize the network’s training loss.
[AS: But isn’t “numbers that happen to work to minimize the network’s training loss” generally what is happening in training LLMs? Training loss is always computed with reference to some known or expected result, and so the resulting coordinates reflect the original goal of the training (e.g., to pick a very specific example used elsewhere on this site, producing embeddings for patent claims to enable prediction of CPC patent classification codes from the text of those claims). But any higher-level features or concepts that may or may not be reflected in the resulting network are still, at bottom, simply “numbers that happen to work to minimize the network’s training loss”. See Andy Clark’s books on connectionism from the 1990s (Microcognition; Being There; Associative Engines) re: “features,” “collective variables,” post hoc explanations of net’s behavior, and mis-attribution of those post hoc features to the net itself. On the other hand, note ChatGPT’s example above of “emergent properties in high-dimensional embeddings (e.g. synonyms clustering together).”]
Temperature, variety, and certainty
Major LLMs—such as those from OpenAI, Anthropic, and others—typically do not publicly disclose the exact temperature value (or other sampling parameters) they use in their hosted, consumer-facing chat apps. Even when an API offers a “temperature” parameter (like OpenAI’s API for gpt-3.5-turbo or gpt-4), the platform can combine that user-chosen temperature with additional techniques — like top-p (nucleus) sampling, repetition penalties, or their own dynamic heuristics. Because of that, there isn’t a single “official” temperature used universally.
In other words, while the concept of “temperature” is central to how an LLM decides which token to generate next:
- Hosted Chat Systems often tune or fix sampling parameters behind the scenes.
- API-based Models may expose user-settable temperature (e.g., 0.7 by default), but the “raw” model might still have internal or supplemental sampling layers.
How It Affects My Current Replies
As ChatGPT, I’m operating under whatever [ChatGPT reply ends right here]
[I press the recycle button to get new reply to same prompt, and choose ChatGPT-4o; I had been on ChatGPT o1]
Temperature Settings in Major LLMs
For major LLMs (like OpenAI’s GPT models, Anthropic’s Claude, Google’s PaLM, etc.), temperature settings are often configurable and depend on the intended application or use case. Here’s how they’re typically handled:
- Default Temperatures:
- Most LLMs in API-based setups use a default temperature of 0.7. This strikes a balance between creativity and reliability, allowing for some variety in output without becoming erratic or inconsistent.
- In fine-tuned models for specific domains (e.g., legal or medical), lower temperatures (e.g., 0.0–0.3) are often used to ensure more deterministic and factually consistent responses.
- Human-Facing Applications:
- For conversational models like ChatGPT, Claude, or others, the temperature may vary depending on the “persona” or “mode” configured for the model (e.g., creative writing vs. technical support). These settings are typically around 0.5–0.8 for general-purpose conversations, though the actual implementation may include more sampling controls like top-p or top-k.
Temperature’s Effect on My Output Right Now
When I reply to your questions in this interface, my output is influenced by OpenAI’s default conversational sampling strategy, which might include: [AS: ChatGPT hedges its statements about its own behavior with “might”, “My responses are likely calibrated to…”]
- Moderate Temperature (~0.7): My responses are likely calibrated to strike a balance between:
- Variety: Offering a range of expressions and explanations when appropriate.
- Certainty: Prioritizing high-confidence, relevant information for factual queries.
- Additional Sampling Techniques:
- OpenAI may combine top-p sampling (e.g., restricting output to the most likely tokens that cumulatively account for p% of probability mass) with temperature to limit overly random choices. This helps ensure outputs are coherent and on-topic.
- Safety mechanisms may further filter or guide responses, overriding purely probabilistic sampling in certain sensitive contexts.
- Dynamic Adjustments:
- While my tone and structure are relatively consistent, OpenAI might tune parameters dynamically for specific questions or user interactions, especially in high-stakes scenarios where accuracy is critical.
Relating This to My Responses
Right now, my replies aim to:
- Be accurate and structured: Avoiding overly speculative or creative tangents.
- Show variety where helpful: For example, offering nuanced explanations or alternative phrasings if I detect ambiguity.
- Maintain clarity and relevance: Prioritizing information that feels most relevant to your question.
In practice, the variety and certainty you observe reflect the system’s calibration—a temperature of around 0.7 combined with guardrails ensures my answers are conversationally flexible while minimizing randomness.
Why 768?; “sweet spot”
Thought for 17 seconds
1) Why “768” for Embedding Dimension?
Many popular language models (including the original GPT-2 “small” model) use 768 as the width of their token embedding and hidden states. This choice (768) is something of a sweet spot for model capacity vs. computational cost in earlier generations of Transformers. It’s not a magic number derived from fundamental principles, but rather a practical design decision made by the model’s creators. Other models use 1024, 1280, 1536, 2048, etc.
- GPT-2 (small): nembd=768, nlayer=12, nheads=12.
- BERT Base: Hidden size = 768, 12 layers.
- BERT Large: Hidden size = 1024, 24 layers.
All of these are just design choices balancing memory, speed, and accuracy.
2) “max_tokens=768” vs. “n_embd=768” Are Unrelated
Even though both can be 768 in code, they represent two different concepts:
- max_tokens (or sometimes max_length, max_seq_len, etc.):
- Defines how many tokens the model will process or generate in a single forward pass (the size of the text “window” or context length).
- For example, a model might handle up to 1024 or 2048 tokens at once. A smaller setting like 768 simply caps how many tokens you allow the model to generate or ingest in one run.
- n_embd (or d_model, “hidden size”):
- Defines the dimensionality of each token’s embedding vector as it flows through the network.
- It does not limit how many tokens can be in the input. Rather, it states the size of the representation for each token.
In other words:
- “max_tokens” is about sequence length (how many tokens can be processed at once).
- “n_embd” (or “embedding dimension”) is about feature width (how many features per token).
They can have the same integer value purely by coincidence or user choice—one sets a maximum sequence length, while the other sets a dimension of the model. There’s no intrinsic reason for these numbers to match.
Concrete Example
- A GPT-2–style model might have:
- Embedding dimension (n_embd) = 768
- Max context length = 1024 tokens
That means each of up to 1024 tokens is represented by a 768-dimensional vector internally. If you configure a generation with max_tokens=768, that just means “don’t produce more than 768 tokens in the output,” while the network’s internal embeddings remain 768-dimensional vectors for each of those tokens.
TL;DR [AS: funny, ChatGPT has learned how and when to use “too long; didn’t read”]
- 768 as an embedding size is a common architectural choice, especially for GPT-2–class models and some BERT variants.
- max_tokens (sequence length) and n_embd (embedding dimension) are completely separate hyperparameters. They can each happen to be 768 but serve different roles.
Backpropagation and the optimizer are distinct
Sure! In neural network training, an optimizer is the algorithm that adjusts the model’s parameters to minimize the loss function. Here’s a breakdown:
1. The Role of the Optimizer
- Forward pass: You feed data x into the model to get a prediction ^y [hat y].
- Compute loss: Compare ^y to the true label y.
- Backward pass: Use backpropagation to compute gradients ∂loss /∂wi for each parameter wi.
- Optimizer step: Update each parameter based on its gradient and some update rule (this is where SGD, Adam, etc. come in).
The optimizer’s job is to figure out how to apply these gradients—how big each update should be, how to handle momentum, or how to adapt per-parameter learning rates.
[AS: I later asked ChatGPT to elaborate:
(1) When you said “compare,” does this include knowing whether the predicted y was higher or lower than the target/actual y?
(2) Can you give me a prose equivalent for the backward pass formula with ∂loss? I assume that’s a delta (diff), but I’d like a brief but complete prose restatement.
ChatGPT:
(1) “Compare” in the Loss Function
Yes — when we say we compare the predicted value ^y to the true label y, we specifically measure how far off the prediction is, and in which direction, by using a loss function. For example:
— In Mean Squared Error (MSE), the network looks at (^y minus y) (the difference) and squares it. That process inherently captures whether ^y is larger or smaller than y because the difference can be positive or negative before squaring.
— In Cross-Entropy (for classification), the loss depends on whether the predicted probability for the correct class is too low or closer to 1, etc.
So yes, the notion of “compare” absolutely includes whether ^y overshot or undershot the actual y. That difference is precisely what the loss function quantifies in a numeric form so the model knows “by how much, and in what direction” it made an error.
(2) Prose Restatement of “∂loss /∂wi”
A more verbose, plain-English way of stating this is:
“Backpropagation computes, for each parameter wi, how much the overall error (the loss) would change if we tweaked wi a little bit.
This tells us the direction and magnitude in which to adjust wi to most effectively reduce the loss.”
— ∂loss∂ /∂wi is the slope of the loss with respect to wi.
— If this slope is positive, we know increasing wi will increase the loss, so we want to move wi down.
— If it’s negative, the opposite is true.
— The absolute value of that slope tells us how sensitive the loss is to changes in wi, guiding the size of the update we apply during optimization.]
2. What Is SGD?
SGD stands for Stochastic Gradient Descent. In its simplest form, it updates each parameter w with:
w ← w − η ⋅ ∇ w loss
[AS: ChatGPT’s later prose restatement: “For each parameter w, we take the current value and subtract (i.e., move in the negative direction of) the learning rate multiplied by the gradient of the loss with respect to . This ensures we move w in the direction that most rapidly reduces the loss.” η (eta) is often used for the learning rate in machine learning; ∇ (“nabla” or “del”) is the gradient operator; ∇loss (“gradient of the loss”) is used to see how each parameter influences the overall loss.]
- η (eta) is the learning rate (e.g., 0.1 in your code).
- “Stochastic” means we often compute the gradient on a small batch of data (rather than the entire dataset at once).
- Pros: Easy to understand, relatively few hyperparameters, often works well with enough tuning.
- Cons: Might converge more slowly or get stuck if the learning rate is not tuned carefully.
You can add features to basic SGD such as momentum (which helps it push through local minima or ravines).
3. What Is Adam?
Adam (short for Adaptive Moment Estimation) is a more advanced optimizer that keeps track of exponentially decaying averages of past gradients and their squares. Each parameter effectively gets its own adapted learning rate. The update equations are more elaborate, but conceptually:
- Momentum: Adam calculates a moving average of past gradients (like momentum).
- Adaptive learning rate: Adam also calculates a moving average of the squared gradients, so parameters that consistently see large gradients get a different (often smaller) effective learning rate, while parameters that see small gradients get a larger effective learning rate.
- Pros: Converges faster in many practical settings, less sensitive to the initial choice of learning rate.
- Cons: Can overfit if not tuned, can get stuck or plateau in some edge cases, requires more hyperparameter tinkering (e.g., β1, β2).
4. Key Takeaways
- SGD is simple and reliable if you tune the learning rate and possibly add momentum.
- Adam is more adaptive and often faster to train large models in practice.
- Both do the same conceptual job: adjust parameters step by step to minimize your loss using gradient information, just with slightly different rules for how big each step should be.
In small toy examples (like your tiny text net), either SGD or Adam can work fine. In large-scale deep learning, Adam or variants like AdamW, Adafactor, and others are extremely common because they often converge more smoothly on big datasets.
Exactly! You can think of backpropagation as the mechanism that computes how each weight contributes to the loss (i.e., it calculates the gradients). Meanwhile, the optimizer decides what to do with those gradients—how large an update to apply to each parameter, whether to use momentum, etc.
In short:
- Backprop: “Here are the gradients: weight w1 should move in this direction by 0.034, weight w2 -0.012, etc.”
- Optimizer: “Great, I’ll apply those updates in a certain way—maybe plain Δw=−η∇w for SGD, or Adam’s adaptive per-parameter steps.”
They work together: backprop figures out which direction to tweak parameters, and the optimizer actually moves them in that direction.
[AS (later follow-up): I had somewhere read someone say that, for each epoch, all weights are moved the same way. That never made sense to me. It sounds like you’ve confirmed that is definitely not true?
ChatGPT:
Correct — each weight is adjusted differently based on its own gradient. Even if they are all updated at the same time (in one “optimizer step”), they do not move in the same direction or by the same amount. Specifically:
— Different Gradients: Each parameter wi has its own partial derivative (∂loss / ∂wi). That derivative can be positive, negative, or very small — completely different from other parameters’ derivatives.
— Separate Updates: If you have, say, 10,000 weights, you’ll get 10,000 different gradient values after backprop. Each weight’s update is
Δ=−(∂loss / ∂). There’s no reason for all 10,000 Δ to be the same sign or magnitude.
— Synchronized Step: What is true is that all weights are updated in the same “step” each epoch (or each mini-batch). But they’re not updated by the same vector—each weight has its own unique adjustment.
— So if someone said, “all weights move the same way every epoch,” they might have been mixing up “all weights get updated at the same moment” with “all weights get updated by the same amount/direction.” The latter is certainly not correct.]
How do transformers & attention relate to basic neural networks?
AS: There’s an earlier subsection:
I think I now need to dive a little more deeply. Can you elaborate on each of the major ways the internal workings of Transformer are “conceptually the same as your toy net,” and then some major ways they are different, even if conceptually the same?
Below is a deeper look at how Transformers (like in GPT, BERT, etc.) share fundamental similarities with your toy neural net—while also highlighting the specialized features that set Transformers apart.
1. Similarities: “They’re All Neural Nets”
- Linear Layers (Matrix Multiplication + Bias)
- In your toy net, each layer does: z=W×(input)+b z = W \times \text{(input)} + bz=W×(input)+b
- Transformers also have linear (fully-connected) layers. In fact, most of the parameters inside a Transformer are in these linear projections, just on a much larger scale.
- Nonlinear Activations
- Your toy net uses ReLU; Transformers often use ReLU, GELU, or similar.
- The fundamental idea remains: a small, element-wise function that introduces nonlinearity.
- Stacked Layers
- Your toy net might have 2 or 3 sequential layers:
Linear -> ReLU -> Linear -> ReLU -> ... -> output. - A Transformer has multiple layers (often called “blocks” or “encoders/decoders”), each containing sub-layers (attention + feedforward). You still have that concept of repeated transformations, each building more complex representations.
- Your toy net might have 2 or 3 sequential layers:
- Parameter Learning via Backprop + Gradient Descent
- The same process: forward pass → compute loss → backprop to get gradients → optimizer updates.
- Transformers just do it at a massive scale (billions of parameters, large datasets).
- Universal Approximation
- A ReLU (or other activation) MLP can approximate many functions.
- Transformers also rely on the same universal approximation principle but add architectural features to handle sequences more effectively.
2. Differences: “Specialized for Sequences and Context”
- Attention Mechanism
- What It Is: Instead of just feeding data forward through linear layers, the Transformer has a sub-layer called self-attention, which dynamically weights different positions in the input sequence based on their relevance to each other.
- Why It’s Different: This lets the model handle variable-length sequences and long-range dependencies far more effectively than a plain MLP or simple RNN.
- Yet Still a “Neural Net”: Attention is built from linear projections (queries, keys, values) and dot products. You still have weights, biases, and an activation at some point. It’s just structured differently.
- Multi-Head Attention
- The Transformer splits the embedding dimension into multiple “heads” that each do their own attention weighting.
- Conceptually, it’s like having multiple “parallel MLP slices” looking at different patterns in the sequence.
- But under the hood, it’s still matrix multiplies + learned parameters + nonlinearity, repeated.
- Positional Encoding / Embeddings
- Transformers do not inherently know the order of tokens in a sequence, so they add positional information (via sinusoidal embeddings, learned embeddings, or other schemes).
- Your toy net for x\sqrt{x}x didn’t have to worry about order—it just had a single scalar input.
- The concept remains that “we feed the input in numeric form,” but Transformers need extra numeric signals to preserve sequence order.
- Residual Connections & Layer Normalization
- Transformers typically have residual (skip) connections around the attention and feedforward sub-layers, and they use layer normalization or batch normalization.
- These help stabilize training in deep architectures and maintain signal flow.
- Your toy net likely just stacked layers without skip connections or normalization. It’s possible to add them in a toy model, but they aren’t essential at small scale.
- Scale & Parallelization
- Transformers are designed to handle massive parallelism on GPUs/TPUs. They often have hundreds or thousands of dimensions in each layer, and can process sequences of hundreds or thousands of tokens at once.
- Your toy net might have 2 neurons in one hidden layer and 2 in the next—trivial to compute on a CPU.
- The underlying math (matrix multiplication) is the same, but Transformers do it on a huge scale.
- Sequence-to-Sequence or Causal (Next-Token) Architecture
- Transformers can be encoder–decoder (like T5, which takes input text and produces output text) or decoder-only (like GPT, focusing on next-token prediction).
- Both are still giant feed-forward networks with attention layers in each “block.” This is a structural difference from a simple feedforward net that processes a single input vector.
- Training Objective
- Your toy net: Minimizing MSE to approximate x\sqrt{x}x.
- Transformers: Minimizing cross-entropy for next-token prediction, or some masked-language modeling objective.
- The concept is the same (error minimization), but the specific loss function is geared to text generation.
- Contextual Word Embeddings
- A big benefit of Transformers is that each token’s representation is updated in context, so “bank” in “river bank” and “bank” in “financial bank” get different internal embeddings.
- Your small net deals with a static input–output scenario. Transformers keep re-computing embeddings at each layer, factoring in attention from other tokens in the sequence.
3. Putting It All Together
- Same DNA:
- Computations revolve around matrix multiplication, biases, and element-wise nonlinear activations.
- We rely on gradient-based optimization (backprop).
- We track and update large sets of parameters.
- Key Distinctions:
- Attention for sequence context, rather than just static feed-forward.
- Positional embeddings so the model “knows” token order.
- Scale: Many layers, large embedding dimension, multi-head attention, etc.
- Residual + normalization for stable, deep training.
- Causal / bidirectional architectures for different tasks (next-token vs. masked token).
TL;DR
- Transformers share the basic building blocks of your toy MLP: linear layers, activations, gradients, training loops.
- They add specialized machinery (attention, positional encoding, multi-head structure, residual connections) to handle long text sequences (or images, code, etc.) efficiently, capturing complex patterns in ways a small feed-forward net simply can’t.
So at heart, Transformers are big neural nets. They just have a unique architecture optimized for sequence modeling, scaling to billions of parameters, and learning rich context from large corpora.
[AS (later follow-up): You’ve several times referred to “MLP”. I know this means Multilayer Perceptron, and am somewhat familiar with the history of perceptrons. But I’m curious if your use of the MLP term here signifies anything different from saying e.g. “neural network”.
ChatGPT:
Yes. MLP (Multilayer Perceptron) typically refers to a specific subset of neural networks that:
— Are fully connected (each neuron in one layer connects to every neuron in the next).
— Use feedforward layers (no recurrent or convolutional operations).
— Stack multiple layers (multilayer).
By contrast, “neural network” is a broader umbrella term for any architecture that uses layers of parameters and nonlinear activations, such as RNNs, LSTMs, CNNs, Transformers, etc. An MLP is just one classic form of a feedforward network.]
Transformers & attention do not employ recurrence
In a strict architectural sense, standard Transformers (the kind at the core of most LLMs) do not have feedback or recurrence loops in the same way an RNN or LSTM does. Instead, Transformers handle sequential data (like a conversation) through:
- Self-Attention over a sliding context window
- Re-feeding previous tokens (including the user’s and model’s own responses) back into the model as new input
So while it may feel like the model is “holding onto state” and “feeding output back as input,” what’s actually happening in most LLM implementations is:
- No direct cyclical data flow inside the model: The raw architecture is still a feed-forward stack of attention blocks; there’s no hidden state carried around from one forward pass to the next.
- Instead, the entire conversation so far—all tokens from user + system + model responses—is appended to form the new “prompt” on each turn. Each forward pass sees the entire context window as input and produces the next token(s). [See earlier note on how this can lead to LLM over-agreement with mis-statements in the user’s prompts.]
1. No “Classical Recurrence” in Transformers
- In RNNs/LSTMs, hidden states get passed from one timestep to the next, creating an explicit feedback loop.
- Transformers compute each token’s representation using attention over all tokens in the current window, but do not pass hidden states forward in a recurrent loop.
2. Conversation History as Input
- In an interactive chat, each new user query and the model’s prior responses are collected into a context.
- That entire sequence of tokens is fed into the model again at each step, typically truncated if it exceeds the maximum context length (e.g., 4,096 tokens, 8,192 tokens, etc.).
Hence, from the user’s perspective, the model “remembers” past turns; from a technical standpoint, it’s just because the old text is still in the input buffer for the next forward pass.
3. Specialized Mechanisms for State (Optional)
- Some advanced or experimental systems attempt to maintain external state across turns in ways other than re-feeding the entire context (for memory or efficiency reasons). That’s an implementation detail external to the basic Transformer block, though.
- The raw Transformer blocks themselves remain feed-forward modules with no built-in cyclical data path.
Bottom Line
Yes, there is a notion of “back-and-forth feedback” in an LLM-based chat, but it’s typically achieved by re-appending prior conversation tokens into each new input—not by a direct recurrent or cyclical connection within the Transformer’s internals. So Transformers stay feed-forward at heart, yet handle conversation by leveraging their large context windows.
[AS (later follow-up): We earlier discussed transformers and “attention.” Does the term “attention” simply refer to getting the net to pay attention to (attend to) something in particular? Or does it have some wider significance, as in William James’s very length chapter on attention in the 19th century classic Principles of Psychology? And why is it said to be “All You Need” in the foundational Attention paper, as if it were love in a Beatles song? Is it really that central/crucial to modern AI like yourself, ChatGPT?
ChatGPT:
1. “Attention” in Transformers Is a Specific Mechanism
When we say “attention” in the context of Transformers (and related deep learning models), we’re referring to a mathematical mechanism that dynamically computes weighted sums of certain parts of the input (or hidden states) based on learned relevance scores (queries, keys, values). This mechanism is:
— Not identical to the everyday psychological concept of “paying attention,” though it’s a loose metaphor.
— Implemented via linear projections and dot products—queries × keys, generating attention weights that are applied to values.
This helps the model focus on the most relevant tokens or features at each step, especially in sequences of text.
2. The “All You Need” Claim
The iconic paper Attention Is All You Need (Vaswani et al., 2017) introduced the Transformer architecture, showing you could build a high-performing language model entirely around attention — without the convolution or recurrence typically used in previous models (like CNNs or RNNs).
— Why They Claimed “All You Need”:
The authors showed that by stacking multiple self-attention blocks (plus feedforward layers, residual connections, and layer norms), you could outperform state-of-the-art models on translation and other NLP tasks faster and with fewer computational constraints than RNN-based or CNN-based approaches.
— Hence “All You Need”: At least for many sequence modeling tasks, attention-based architectures alone can do extremely well — no recurrent loops or specialized convolution layers necessary.
3. Is It Really That Central?
Yes, in modern NLP and many other domains, attention-based (Transformer) models have become the dominant architecture:
— Scale: Transformers scale better with data and parameters, leading to the massive LLMs (like GPT-3.5, GPT-4, Claude, PaLM, etc.).
— Parallelization: Unlike RNNs, Transformers can process tokens in parallel (using self-attention), which is more efficient on GPUs/TPUs.
— Performance: Empirically, they excel at language understanding and generation, code generation, speech tasks, even images (Vision Transformers), etc.
In short, attention is a key ingredient that unlocked the rapid progress in large language models and many advanced deep learning systems. It doesn’t necessarily have the philosophical depth that William James wrote about (“What does it mean to truly attend to something cognitively?”), but the name highlights that the model is “learning to weigh different parts of the input differently” — some token positions get more weight (attention) than others, context by context.
4. Bottom Line
— Term “Attention”: A specific, learnable weighting mechanism, not directly the same as human cognitive attention (though inspired by that concept).
— Revolutionary: Because attention-based Transformers decoupled the bottlenecks of recurrence and made large-scale language models possible.
— “All You Need”: The Transformer architecture’s reliance on attention (plus feedforward layers, etc.) has proven enough to handle a wide array of tasks extremely effectively, which is why it’s considered central or “all you need” for many modern NLP achievements.
]
Getting unstuck from local minima
Below, ChatGPT gives me some advice about why technically correct neural-net code nonetheless might not be working as desired; I push back against a mistake ChatGPT makes; it somewhat defensively explains what nonetheless remains true and important about what it said; we see how there’s some parameter tweaking involved with even a ridiculously small example, generally touch on desirable properties for trained neural nets, e.g. “find a parameter setting that satisfies all pairs more easily” and “nudge the model to a different minima,” and introducing variety into next-word prediction, rather than simply picking the most-probable next word.
>>> while (s != “!”):
s = manual_forward(s)
For a reason I don’t understand, it can get stuck in an endless loop of dog->dog . I’ve put the revised .py file at: GitHub Gist link to edited “stuck” tiny_text_net.py
— can you take a look and see what I’ve done wrong?
ChatGPT:
Stopping Conditions [very lengthy CoT below while ChatGPT examines the .py file:]
Analyzing the code
I’m looking into the code snippet provided, considering potential causes for the endless loop and potential fixes. Progress is being made in identifying the issue.
Working through loops
I’m examining a snippet of code that imports packages, defines a model, and runs a training loop to compare output and target pairs. Progress is steady.
Identifying potential causes
I’m analyzing why the loop might be stuck, considering repeated or contradictory pairs, and noting that without convergence, the mapping for “dog” might just map to itself.
Analyzing training dynamics
It’s worth noting that repeated pairs can disrupt training. Focusing on increasing hidden dimension and training epochs could greatly improve performance.
Assessing impact
I’m examining how tweaking the learning rate, enhancing training duration, or incorporating random seed could mitigate loop issues. Repeated pairs and inadequate training data are also critical factors.
Seeking solutions
I’m working through training dynamics, like the need for more epochs or data randomization, to clarify the sequence and prevent the loop from sticking on dog->dog.
Assessing convergence
I’m recognizing that the network may struggle with convergence due to the small dataset size and single-pass epochs, making improvements like higher dimensions or smaller learning rates necessary.
Identifying conflicts
It’s becoming clear that the network might confuse “dog” as both an input and label for different pairs, which could lead to “dog” outputting “dog” instead of “!” or another token.
Identifying challenges
It’s worth noting that the network’s lack of convergence to a “dog” mapping may stem from contradictory pairs, limited capacity, stuck training, or the need for data randomization and improved training methods.]
I took a look through your revised TinyTextNet code (the gist at your link). The short version is that there’s no obvious bug in your Python script—it runs and trains “as intended.” The infinite dog → dog loop happens because your tiny net is simply learning a parameter configuration that maps “dog” back to “dog” instead of mapping “dog” to “!” as you hoped.
Below is a more detailed explanation of why this can happen—and some things you can try to fix it.
1. Why the Net Might Predict Dog→Dog
- Small Capacity
- You’re using a minuscule network:
- Embedding dim = 2
- Hidden dim = 2
- It has only a handful of parameters to learn all your mapping pairs, including “dog → !” but also “silly → dog” and “cat → dog,” etc.
- The net can get “confused” because “dog” is both an output class in some pairs (cat→dog, silly→dog) and an input in others (dog→?). It may settle on a local minimum where it repeatedly predicts “dog” for “dog.”
- You’re using a minuscule network:
- Conflicting or Repetitive Training Pairs
- You have
pairsthat overlap or repeat. For instance, you have two entries for(dog→!)and two entries for(world→!). [AS: actually no, the code does NOT look like that. Not everything intelligent-sounding is actually intelligent (though I still say it’s remarkable how intelligent ChatGPT and its brethren behave on a foundation of (as we’re discussing in this article) next-word prediction.] - A tiny net might struggle to handle these “repeated” constraints or not converge robustly in such a small parameter space.
- You have
- Plain SGD, Single-Learning-Rate
- You are using
optim.SGDwithlr=0.1. That can work, but it might also converge to a suboptimal local minimum, especially with a small net and a small dataset that’s repeated each epoch. - Sometimes using Adam or SGD + momentum can help escape local minima.
- You are using
- Number of Epochs and Training Order
- You run 501 epochs over the same small batch of 8 pairs. While that seems sufficient, it might still land in a local solution (like dog→dog).
- Also, if you never shuffle or randomize anything, gradient descent can get stuck in a pattern.
So, in short, the code is correct in the sense that it’s “doing what you told it to do.” It’s not guaranteed to memorize “dog→!” with such a small architecture and a single repeated batch.
2. How to “Fix” or Avoid the dog→dog Loop
If you want the model to robustly learn “dog→!” (and the other mappings), here are some tweaks to try:
- Increase the Model Capacity
- For instance, use
embed_dim=4orembed_dim=8, andhidden_dim=4or higher. A slightly bigger net may find a parameter setting that satisfies all pairs more easily. [AS: note what ChatGPT is helping me do here: nudging, satisfying all input text words at the same time.]
- For instance, use
- Use Adam
- Instead of
optim.SGD(model.parameters(), lr=0.1), try:optimizer = optim.Adam(model.parameters(), lr=0.01)Adam often converges more smoothly on small tasks with weird overlaps.
- Instead of
- Add More Epochs / Lower LR
- Sometimes dropping the learning rate (e.g.,
lr=0.01) and going for more epochs can help nudge the model to a different minimum.
- Sometimes dropping the learning rate (e.g.,
- Remove Duplicate/Redundant Pairs
- You have
(dog->!)repeated twice,(world->!)repeated twice, and “cat->dog,” “silly->dog,” etc. - Try a simpler set of unique pairs or break them into a small “dataset” with some variety.
- You have
- Shuffle the Data
- Right now you feed all the pairs in a fixed order, each epoch. In real training, you’d typically shuffle or sample mini-batches. That randomness can help avoid local minima.
- Debug with a Print of Final Predictions
- After training, print out the final logits for each input token. You may see that “dog” is predicted to have its highest logit for “dog,” confirming it got stuck.
3. Why the Manual Forward Pass Can Get Stuck in a Loop
Your last lines:
s = "hello" while (s != "!"):
s = manual_forward(s)- If “dog→dog” is the learned mapping, once the model hits “dog,” it’ll keep predicting “dog,” never reaching “!” to break out of the loop.
- That’s not a “bug” in the loop logic—it’s just that the network outputs “dog” again, so
snever becomes!.
4. Bottom Line
- The snippet isn’t broken per se—the net is just stuck in a local minimum.
- There’s no guarantee a small 2×2 net can perfectly memorize all token pairs you gave it.
- Try using a slightly bigger network, a more advanced optimizer (like Adam), or removing duplicate pairs. That should help the model converge on the desired dog→! mapping instead of dog→dog.
Once you make those adjustments, you should see the infinite loop vanish, and “dog” will predict “!” as intended.
pairs = [
(token2idx[“hello”], token2idx[“world”]),
(token2idx[“cat”], token2idx[“dog”]),
# maybe a couple more so there’s something to learn
(token2idx[“dog”], token2idx[“!”]),
(token2idx[“silly”], token2idx[“dog”]),
(token2idx[“cute”], token2idx[“cat”]),
(token2idx[“world”], token2idx[“!”]),]
?[If something about an AI chatbot’s response doesn’t look quite right, ask the AI chatbot to explain it]
I took another look at your gist code, and you’re right — there is not an actual duplication of (dog->!) or (world->!) in that snippet. My earlier mention of duplicates was likely based on a misread or a different snippet. In the code you pasted:
pairs = [ (token2idx["hello"], token2idx["world"]), (token2idx["cat"], token2idx["dog"]), (token2idx["dog"], token2idx["!"]), (token2idx["silly"], token2idx["dog"]), (token2idx["cute"], token2idx["cat"]), (token2idx["world"], token2idx["!"]) ]There are indeed no exact duplicates like (dog->!) repeated more than once. So let me restate the underlying issue more accurately: [AS: ChatGPT slowly works its way to essentially saying “what I really meant to say is still true and important”]
- Multiple pairs feed into the same output “dog.”
- You have
(cat->dog)and(silly->dog). - This alone can be tricky for a very tiny net to handle, because “dog” is a target token for multiple inputs.
- You have
- “dog” also appears as an input token that’s supposed to map to “!”
- So the network must learn that when it sees “dog” as input, it should predict “!”. But at the same time, it has multiple inputs that all map to “dog.”
- Net capacity might be too small (2D embeddings, 2D hidden layers) to juggle all these relationships reliably.
- It can easily learn “cat -> dog” and “dog -> dog” instead of “dog -> !,” because it sees “dog” so often as a target. That local minimum satisfies some constraints but not all.
Hence, the rest of the explanations still apply:
- The model can get stuck mapping “dog” back to “dog” because that’s one local solution that partially satisfies the training data (though it’s wrong for the pair
(dog->!)). [AS: altered weights/biases during training that partially satisfy some of the training data can get solidified in the final model.] - Using a bigger net, a different optimizer, or shuffling data might help it converge on
(dog->!)properly.
Bottom line: There’s no literal duplication in your final snippet, so apologies for the confusion there. The “dog→dog” loop is just a local-minimum artifact from the model’s limited capacity and the somewhat overlapping relationships in the pairs.
Yes! The simplest approach is to not always pick the argmax token, but rather sample from the probability distribution the model produces at each step. When you do pred_token_idx = torch.argmax(logits, dim=-1).item(), you always pick the highest logit, which yields a deterministic (and thus repetitive) outcome.
Below is one straightforward way to introduce randomness (a “temperature” effect) in your tiny net’s output generation.
1) Replace Argmax with Sampling
Right now, your code for predicting the next token might look like:
pred_token_idx = torch.argmax(z_out).item()To add variability, do something like this:
import torch.nn.functional as F
def sample_token(logits, temperature=1.0):
“””Given a 1D Tensor of logits for each token, sample a token index.”””
# Scale logits by 1/temperature
scaled_logits = logits / temperature
# Convert to probability distribution via softmax
probs = F.softmax(scaled_logits, dim=-1)
# Draw one sample from that distribution
sampled_idx = torch.multinomial(probs, 1).item()
return sampled_idx
def manual_forward_with_sampling(token_str, temperature=1.0):
x_idx = token2idx[token_str]
x_tensor = torch.LongTensor([x_idx])
with torch.no_grad():
# Normal forward pass
emb_vec = model.embed(x_tensor) # [batch_size, embed_dim]
h1 = F.relu(model.fc1(emb_vec))
h2 = F.relu(model.fc2(h1))
z_out = model.fc_out(h2).squeeze(0) # shape [vocab_size]
# Instead of argmax, we sample:
pred_token_idx = sample_token(z_out, temperature)
return idx2token[pred_token_idx]
Then in your loop:
s = “hello”
while (s != “!”):
s = manual_forward_with_sampling(s, temperature=1.0)
print(s)
How It Works
- We scale the logits by 1/temperature.
- If
temperature < 1, the distribution gets sharper (the largest logit is more likely). - If
temperature > 1, the distribution gets flatter (less difference between high and low logits, so more randomness).
- If
- We take a softmax of these scaled logits to get probabilities.
- We sample from that probability distribution with
torch.multinomial(probs, 1). - That sampled token might not be the highest logit, which creates variety.
2) Tuning Temperature
- Lower temperature (e.g., 0.6 or 0.7) → more consistent, but still occasionally picks a lower-prob token for variety.
- Higher temperature (e.g., 1.2, 1.5) → more random, potentially nonsensical outputs.
- Exact argmax is effectively the same as temperature →0\to 0→0 (or simply picking the max logit every time).
3) Consider More Capacity or Data
Even with sampling, a very small net might still produce repetitive patterns or “safe” guesses. You’ve already bumped up to embed_dim=4 and hidden_dim=4; you could try 8 or 16 for each, or add more training pairs. That can also give the net more room to learn varied mappings and avoid single “dominant” transitions (like “hello→world!” over and over).
4) Recap
- Why you’re seeing repetitive output: Argmax leads to deterministic picks from the model’s distribution, so if “hello→world→!” is strongly learned, it never deviates.
- How to fix: Use sampling with a chosen temperature to add randomness.
- Result: You’ll still see “hello→world→!” some of the time, but with the right temperature you should occasionally see other transitions.
That’s the essence of how “creative” text generation works in larger LLMs as well: they sample from the softmax distribution rather than always taking the single most likely token at each step.
AS: I feel stupid having asked my question, given we had just had a discussion of temperature and recently discussed argmax. I’ll add in the code you provided. Thank you!
ChatGPT:
No worries — it’s totally normal to ask the same or similar questions as you piece everything together. Good luck with adding in the sampling code, and feel free to tweak the temperature until you get the variety you want!
I asked Google Gemini for a summary of this article, after uploading a PDF to Google Drive:
The document “walking_neural_nets_part2.pdf” is the second part of an article series on understanding how neural networks work, specifically in the context of text processing. It builds on the concepts introduced in Part 1, which focused on “walking” a small neural network that approximated the square root function. Here’s a summary of the key topics covered in Part 2:
- Extending “Net Walking” to Text: The article expands the concept of “walking” a neural network (tracing an input through the network’s layers) from numeric data to text data. It explains that while the underlying network still operates on numbers (weights and biases), the text is represented by numeric vectors called “embeddings.” It emphasizes that the network itself works with weights and biases, and not with the text itself.
- Tiny Text Net Example: The article includes a practical example of a small neural network trained on a tiny vocabulary (hello, world, cat, dog, !). It walks through the process of creating this network in PyTorch, training it, and then manually performing a forward pass (the “walking” process) to see how the input “hello” gets transformed into the output “world.” This example demonstrates how text is converted into embeddings, processed by the network’s layers, and then converted back into text.
- Relationship to LLMs: The article discusses how the concepts learned from these small examples are applicable to Large Language Models (LLMs) like ChatGPT. It explains that while LLMs are much larger and more complex, they still operate on the same fundamental principles of function approximation (mapping an input to an output). The main differences lie in the scale (number of parameters and training data), the complexity of the input/output domains (text sequences instead of single numbers), and the use of specialized architectural features like attention mechanisms.
- Embeddings: Embeddings are discussed in more detail, explaining that they are numeric representations of text (or other data) that capture semantic relationships. In the toy example, the embeddings are simple 2D vectors, while in real LLMs, they are high-dimensional vectors (e.g., 768 dimensions or more) that try to capture much more complex and varied information about words.
- Logits and Softmax: The article explains logits (the raw output of the network before normalization) and softmax (a function that converts logits into probabilities). It clarifies how these are used to choose the next token in text generation.
- Temperature: Temperature, a parameter that controls the randomness of text generation, is explained. Lower temperatures make the output more deterministic (always picking the most likely token), while higher temperatures make it more varied (sampling from the probability distribution).
- Backpropagation and Optimizers: The article distinguishes between backpropagation (which calculates the gradients of the loss function) and optimizers (like SGD and Adam, which use these gradients to update the network’s parameters).
- Transformers and Attention: The article explains how Transformers, the architecture behind most modern LLMs, are similar to basic neural networks in their use of linear layers, activations, and gradients, but also introduces specialized features like attention mechanisms, positional encodings, and multi-head attention to handle sequences and context more effectively. It also emphasizes that Transformers do not employ recurrence.
- Local Minima and Training: The article addresses the issue of a model getting stuck in a local minimum (a suboptimal solution during training), especially relevant in the context of the toy example. It provides suggestions for avoiding this, such as increasing model capacity, using different optimizers, and shuffling the training data.
In essence, Part 2 of the article provides a more in-depth exploration of how neural networks handle text, bridging the gap between simple examples and complex LLMs. It explains the fundamental concepts that underpin all these models and explores some important practical considerations for training and using them.
This summary hits everything I thought important in my Part 2 bullet list towards the beginning of this article, except for:
- Historical comparison of finding square root by guessing/iterating, with the neural net’s method of training/error-adjusting weights
- The centrality of error-correction (nets may be doing pattern recognition, but the way they get there is via error correction)
- The 768 “sweet spot”
Other forthcoming topics on reverse engineering AI here at SoftwareLitigationConsulting.com will include: [[TODO: below is identical to end of Part 1; change to incorporate what’s newly learned in Part 2; note change to “Error correction is (almost) all you need”: part 1 by implication focused only on training, not on net’s use?]]
- Do neural networks truly discover “features” implied or inherent in their input data, and how?
- InterpretableNeuralNet: Explainable AI (xAI) and neural network interpretability with activation capture, hooks, local linear approximation, sensitivity analysis, extracting surrogate coefficients, visualizing layer activations with heatmaps, showing the “top” activated neurons, etc.
- “Error correction is (almost) all you need” (cf. W. Ross Ashby: “The whole function of the brain is summed up in: error correction”); it’s said that “these modern AIs essentially do pattern recognition & pattern matching,” and that’s true of their effect, but that isn’t quite what the underlying neural network is doing: it’s error correct in training; then in use, it’s trying to match new inputs with ones it already knows, so yes, that’s pattern matching, but using vector arithmetic based on embeddings?
- Neural networks, regression, and the Universal Approximation Theorem (UAT)
- AI chatbot “Chain of Thought” (CoT) and “introspection”
- Using sentence embeddings for patent claims to model geometric “spaces” into which patent claims (and corresponding technology) fit
- Developing an offline/local source-code examiner with open-source code-specific LLMs such as CodeLlama
- The relation of interpretable AI, explainable AI, and alignment on the one hand, with software reverse engineering on the other hand
- AI as both a tool in, and subject of, intellectual property litigation